contact : Marion Delehaye (marion.delehaye@femto-st.fr)
News
09/09/2025: Our work on "A framework for continuous superradiant laser operation via sequential transport of atoms" now on arXiv!
03/04/2025: Martina Matusko defended her PhD thesis. Congratulations Martina!
19/03/2025: Martin Hauden defended his PhD thesis. Congratulations Martin!
11/03/2025: our paper on "Offset sideband locking to iodine for laser cooling on the 1S0 → 3P1 transition of 171Yb" just published in Optics Express!
Ultra-stable superradiant laser based on ytterbium atoms
Overview
Our group at FEMTO-ST (Besançon, France) is developing an ultra-stable continuous superradiant laser based on the ¹S₀ → ³P₀ clock transition of ytterbium. This experiment combines two key tools of modern time and frequency metrology: an ultracold atomic sample and a high-finesse optical Fabry–Perot cavity. The goal is to generate a continuous, ultra-stable optical signal with unprecedented frequency stability.
Context: From Timekeeping to Superradiant Lasers
Time and frequency metrology has evolved dramatically over the past decades. From astronomical observations to the 1967 redefinition of the SI second based on cesium atomic transitions, modern clocks have become versatile tools for telecommunications, fundamental physics, and precision measurement.
Current state-of-the-art optical clocks are passive clocks, relying on a laser pre-stabilized to an optical cavity and locked to an atomic reference (ultracold neutral atoms or trapped ions). In contrast, active optical clocks emit light directly from the atomic ensemble via superradiance, without an external laser [1]. Recent pioneering experiments in strontium have demonstrated ultra-stable light pulses [2, 3], and theoretical studies predict that superradiant lasers could reach fractional frequency stabilities below 10⁻¹⁸ τ⁻¹/² [4].
The FEMTO-ST Superradiant Laser Experiment
We are building a superradiant laser with ultracold ¹⁷¹Yb atoms (T ≈ 10 μK) held in an optical lattice inside an ultra-stable Fabry–Perot cavity (σᵧ(τ) ≈ 10⁻¹3).
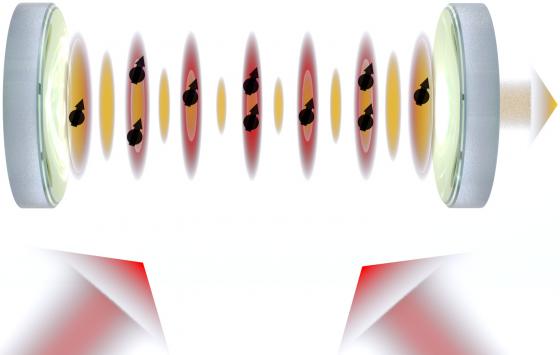
Superradiance is a collective emission phenomenon: when N atomic dipoles oscillate in phase, the emitted intensity scales as N² rather than N, dramatically enhancing the radiation compared to independent atoms. In our setup, the cavity selectively couples the atoms to a single electromagnetic mode, ensuring synchronized emission. In the “bad-cavity” regime (κ ≫ g ≫ γ), photons leave the cavity before being reabsorbed, making the emitted frequency largely insensitive to cavity fluctuations. Using optical pumping, this emission can reach a steady-state, without being limited by pulse duration.
Fig. 1 : Working principles of a superradiant laser. N atoms are placed inside an optical Fabry-Perot cavity tuned to the clock transition wavelength in order to maintain in-phase oscillation between the atomic dipoles. Emitted superradiant photons constitute the ultra-stable signal source.
Current Status:
Cold atom preparation and optical lattice trapping are operational.
Fabry–Perot cavity alignment and characterization are ongoing.
Preliminary atom–cavity coupling measurements have started.
Next Steps:
Transport of cold atoms into the cavity and observation of the first superradiant pulses.
Implementation of controlled superradiant lasing with state preparation and repumping schemes.
Development of continuous operation using sequential loading of atomic ensembles.
Metrological characterization of the superradiant laser output, including stability and spectral measurements.
Opportunities
We are looking for motivated master interns and PhD students to join the project. An MSCA PhD scholarship is available for eligible candidates, within the QuRIOUS network (www.quriousclocks.eu). Please contact marion[dot]delehaye[at]femto-st[dot]fr
References
[1] Prospects for a millihertz-linewidth laser, D. Meiser, Jun Ye, D. R. Carlson, and M. J. Holland, Phys. Rev. Lett. 102, 163601 (2009).
[2] Superradiance on the millihertz linewidth strontium clock transition, M. A. Norcia, M. N. Winchester, J. R. K. Cline and J. K. Thompson, Science Advances 2, 1601231 (2016).
[3] Frequency measurements of superradiance from the strontium clock transition, M. A. Norcia, J. R. K. Cline, J. A. Muniz, J. M. Robinson, R. B. Hutson, A. Goban, G. E. Marti, J. Ye, and J. K. Thompson, Phys. Rev. X 8, 021036 (2018).
[4] Ultimate stability of active optical frequency standards, G. A. Kazakov, S. Dubey, A. Bychek, U. Sterr, M. Bober and M. Zawada, Phys. Rev. A 106, 053114 (2022).
Our group's publications
- A framework for continuous superradiant laser operation via sequential transport of atoms, J. El Badawi, M. Delehaye, B. Bellomo, arXiv:2509.07833 (2025).
- Offset sideband locking to iodine for laser cooling on the 1S0→3P1 transition of 171Yb, M. Hauden, J. Millo, M. Matusko, F. S. Ponciano Ojeda, Y. Kersalé, M. Delehaye, Optics Express, 2025, 33 (6), pp.12519 (2025).
- Superradiant active optical atomic clocks: motivations and current challenges, M. Matusko and M. Delehaye, J. Phys.: Conf. Ser. 2889 012045 (2024).
- Fully digital platform for local ultra-stable optical frequency distribution, M. Matusko, I. Ryger, G. Goavec-Merou, J. Millo, C. Lacroûte, E. Carry, J.-M. Friedt and M. Delehaye, Rev. Sci. Instrum. 94, 034716 (2023).