In Construction... to read more...
Multiscale Model Derivation by Symbolic Computation
| A framework for computer-aided derivation of multi-scale model is under development. It relies on the combination of asymptotic methods used in the field of partial differential equations with term rewriting techniques coming from computer science. In our approach, a multi-scale model derivation is characterized by the features taken into account in the asymptotic analysis. Its construction starts from a multi-scale model derivation of reference, corresponding to a very simple nominal problem, which is transformed to successively take into account all wanted features. So, in addition to the model derivation of reference, the derivation framework includes first order rewriting principles to achieve asymptotic model derivations, and second order rewriting principles for their transformations. The method will be able to generate a family of homogenized models for second order elliptic equations with periodic coefficients including thin domains and strongly varying coefficients. This principles are being implemented in the software package MEMSALab. |
Multiscale Modeling and Control of Cantilever Arrays
| Two-scale models both for one-dimensional and two-dimensional cantilever arrays are developped with possible applications to Atomic Force Microscope Arrays. Their derivation rely on an asymptotic analysis for thin elastic structures and a two-scale convergence for strongly heterogeneous periodic systems. Some models are implemented in the dedicated software package AFMALab together with distributed control implementations based on our distributed computing strategies as well as an algorithm for measurement of cantilever displacements by interferometry. A link has also been implemented to the in-house robust optimization package SIMBAD. |  |
Multiscale Modeling for Wave Propagation
| A dedicated time-space two-scale transform allows to capture the high and low frequency waves in the asymptotics of the periodic homogenization of the wave equation. The asymptotical solution is the sum of the solution of known homogenized equations and of Bloch waves. The coefficients of the Bloch waves are solution to transport equations. |  |
Multiscale Modeling of Periodic Distributed Analog Circuits
| Any number of connected components, crossing and non crossing lines, connected or non connected cells are allowed; currents, branch voltages, node potentials are provided; macro equations are PDEs, micro equations are circuits equations. A good agreement has been demonstrated with the original system; approximation quality increases when the number of cells increase. | 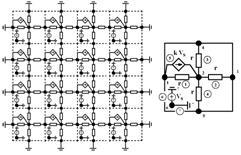 |
Diffusive Realization
| A theoretical framework of diffusive realization has been introduced for state-realizations of linear operators that are solution to certain linear operator-differential equations in bounded domains. The theory has been applied to a Lyapunov equation arising from distributed optimal control. Numerical methods have been established and a first implementation on a FPGA has been achieved. This method is a good candidate for distributed computing implementation of real-time distributed optimal control in large system arrays. |  |
Semi-decentralized Approximations of Riccatti Equations for Distributed Control
| A method has been introduced to realize semi-decentralized optimal control of large linear distributed systems for real-time applications. It applies to systems modeled by linear partial differential equations with observation and control distributed over the whole domain. This is a strong assumption, but it does not mean that actuators and sensors are actually continuously distributed. Models satisfying such assumption may be derived from homogenization of systems with periodic distribution of actuators and sensors. The method is based on a functional calculus for self-adjoint operators. It has been shown to be well suited for being implemented with distributed periodic analog circuits. | 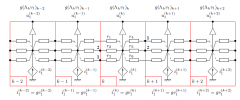 |
